AM/FM ALGORITHMS FOR AUTOMATIC DETECTION AND
PREPARATION OF APPLICATION PLANS
Ibrahim BAZ1 and Ismail
Rakıp KARAŞ1
ragib@gyte.edu.tr,
ragib@gyte.edu.tr
1Department of
Geodetic and Photogrammetric Engineering ( gyte.edu.tr/jeodezi ),
Gebze Institute of
Technology, Gebze , Turkey
Throughout the years
much focus has been placed on developing AM/FM/GIS software packages and
various techniques for data conversion and maximing
its quality. Although data is undoubtedly the foundation-stone of an AM/FM/GIS, it is not possible to judge the success of
the whole system by its data quality and design. The eventual success of the
system will be measured with its ease of use and presentation through
applications. In competitive business environment, software developers face the
urgent need to automate engineering, administrative and public relations
activities in order to make the system easy and user-friendly. One of the most
time consuming and much care needed applications or activities at
municipalities and similar organizations is the preparation of application
plans showing size and boundaries of a parcel and/or boundaries of building
areas. This paper examines how these activities are
being carried out at above mentioned organizations in
1. INTRODUCTION
Computer Aided Design and Drafting (CADD)
technology is a system that supports computer aided mapping. Automated Mapping
/ Facility Management (AM/FM) systems are CADD based systems, and define
relationships among utility system components. Together with the utility
systems attribute data stored in a separate data table, it is possible to
model and analyze a utility systems operation. Geographic Information System
(GIS) is similar to CADD and AM/FM in that it references graphic data elements
to a geographic coordinate system and, similar to AM/FM systems, stores
attribute data associated with the spatial data.
GIS differs from CADD and AM/FM in that the
spatial relationships among all data elements are defined. GIS is best suited
for the analysis of geographic data. Analysis, management and organization of
all kinds of spatial data forms are the subject of GIS [Korte,1997].
All these systems are not contrary to each
other. On the contrary; CADD, AM/FM and GIS systems are components to one
another.
Throughout the years; various data processing
techniques, CADD or AM/FM algorithms and many software packages were developed.
Much focus on these developments has been placed on automation of engineering,
administrative and public relation activities.
Preparation of plan of building boundaries within a
parcel is one of the most time consuming and much care needed engineering work
of the municipalities. Some programs in
Another approach to solve this kind of problem
is to create suitable algorithms and databases which cover all these steps in one
action. This kind of fully automated systems requires detailed analysis and
questioning algorithms.
2. SOFTWARE
DEVELOPMENT
A computer programme
(PLAN_PLOT) was developed. This programme prepares
plan of building boundaries within a parcel or a block suitable for zoning
application, and it carries out this task in fully automated manner. Algorithms
of the programme have been developed
in such a way that boundaries of building within a given parcel are
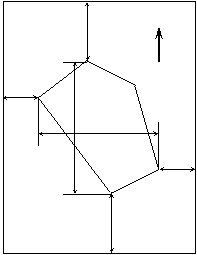
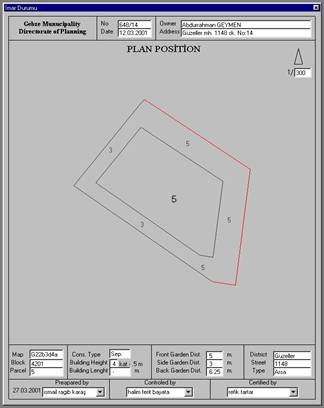
automatically drawn. Figure1 shows a sample output of the programme
run in this respect. This programs run is also designed interactively,
but it only requires parcel numbers for interactive data entry. Rest of the
data such as parcel geometry, building and zoning principle, etc. needed for
plotting are obtained automatically from a database that should be created at
once.
Figure 1: Sample output
of the programme PLAN_PLOT
This database consist of two kinds of table (Fig. 2). One
of these tables consists of parcel numbers and coordinates of corner points,
and the other one consists of parcel numbers, building and parcel principles
respectively.
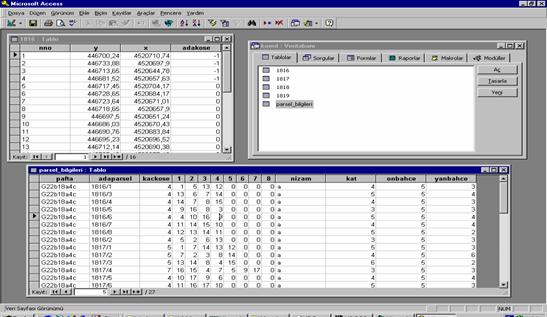
Figure 2: Database
formats
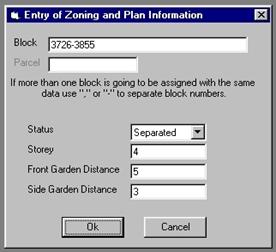
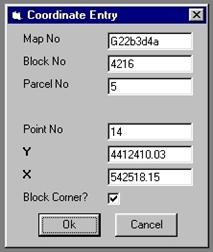
Data entry to these tables can
be done manually or automatically. Details for automatic data
entry process is given in Baz and Karas [2001]. Figure 3 shows sample interfaces for
manual data entry. Building and parcel principles such as type, storey,
front-back-side garden distances, etc. of building may be the same for some
blocks. The PLAN_PLOT notices this fact, and requires only the block numbers
which are to be assigned with the same principles. As for the graphical data
entry, map, block and parcel numbers, coordinates of corner points are stored
manually as shown in Figure 3.
Figure 3: Manuel data
entry and interfaces for them
Data editing can be done on these tables
directly as well as interactively. Interactive editing is carried out on screen
out put. With this editing, all changes are automatically put in action and
stored in related data base tables.
3. ALGORİTHMS
Following are some of the algorithms developed
for the programme PLAN_PLOT.
3.1 Algorithm
For Parcel Drawing Settlement For a Given Scale
This algorithm was developed for settling a
parcel drawing in the middle of plotting area with a changeable scale.
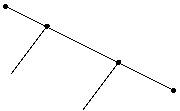
Assuming that parcel to be plotted (Fig. 4) has
corner points 1,2,3,4,5, and point 1 has the smallest Y-coordinate, point 4 has the biggest Y-coordinate, point 5
has the smallest X-coordinate, point 2 has the biggest X-coordinate, and
|
e
N l 2 3
k 1 v
b u
k
4 5 l
plotting area Figure 4: Parcel drawing settlement for a given scale |
e = width of the plotting area * scale b = length of the plotting area * scale Yn , Xn = are mapping coordinates Yn , Xn
= screen coordinates Then following algorithms can be written. u=Y4-Y1 , v=X2-X5 k=(e-u)/2 , l=(b-v)/2 ,and Yn=[Yn-(Y1-k)]
/ scale Xn=[Xn-(X5-l)]
/ scale |
3.2 Algorithms
For Defining Parcel Lines
3.2.1 Definition of Interval Parcel Lines
In this situation, a parcel has three sorts of
line positioning. That can be front, back and side line positioning. This
algorithm was developed to find out these positionings,
and the followings are the procedure to do this.
1. Corner point of a block in which a
parcel exists are obtained from the data base.
2. Line equations of the block are
formed.
3. Parcel corner points which prove
these equations correct are defined.
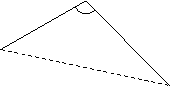
4. Line or lines connecting these
points which are immediately following one another are accepted as front line
or lines of the parcel (Fig. 5).
|
A(p,k)
D B(u,t) |
(y-k) / (k-t)
= (x-p) / (p-u) ise; y =
((k - t) / (p - u)) x + ((tp-uk)/(p-u))
m n |
Figure 5: Determination
of front lines of a parcel
5. Lines connecting remaining parcel
points are accepted as back and side lines of the parcel.
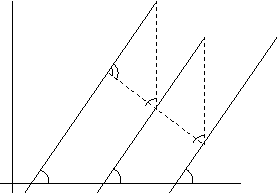
6. Bearing angle between lines which
are formed by connecting any two of these points immediately following one
another are determined.
7. Points with two smallest bearing
angles are accepted as turning points from a side line to a back line and
vice-versa.
8. Line or lines between these two
points are accepted as back lines, and the others as side lines (Fig. 6)
|
C
b α
A
a c B |
s = ( a+b+c ) / 2 tan (a/2) =Ö( ((s-b)(s-c)) / (s*(s-a)) ) |
Figure 6: Determining
back lines of a parcel
3.2.2 Definition
of Corner Parcel Lines
In this situation a parcel has two line
positioning. Those are front and side line positioning. This algorithm was
developed to find out these positionings, and the
followings are the procedure to do this.
1. First four steps of the previous
procedure are applied, and front lines of the parcel are determined.
2. Bearing angles between the first and
the last front lines are determined.
3. If magnitude of a bearing angle is
found to be less than 120º, then parcel is accepted as one of the corner
parcels of the block. (Fig. 7)
4. Fifth step of the previous procedure
is applied.
|
1
a1 a2 3 q b
a3
a4
4
g an n
parcel |
Sum of inner angles of polygon(1,2,3,4,
n) = (n-2)*180° q = b+g-180°
n b+g = Sa - (n-2)*180°
1
n q = Sa - (n-1)*180° 1 |
Figure 7: Definition of
corner parcel
3.3 Algorithm
For Formation of Parallels to Parcel Lines At a Given Distance
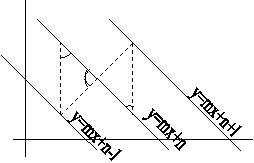
If building approaching distance to parcel
lines given, then this algorithm determines and draws parallels to the parcel
lines at these distances (Fig. 8)
|
l a l s
a a a (a) |
First case: m>0
(a<90º) s = approaching distance l=s/(cos a)
; a=arctg(m) y=mx+n and y=mx+n±(s/(cos(arctg m))) |
|||
|
a-90º s
l l
s a-90º (b) |
Second case: m<0
(a>90º) l=s / (sin (a-100g)) sin (a-100g) = -cos a y=-mx+n and y=-mx+n±(-s/(cos(arctg m))) |
Figure 8: Formation of
parallels to parcel lines at a given distance
3.4 Algorithm
For Determining Corner Points of a Building Drawing
This algorithm determines corner
points of a building drawing. These points are obtained by determination of
cutting points of the immediately following parallel lines described above. If
y = m1x + n1 and y = m2x + n2
represents equations of two lines then coordinates of cutting points of these
equations can be determined via the following equations.
y = ((n2-n1) / (m1-m2))
m1 + n1
, x = ((n2-n1) / (m1-m2))
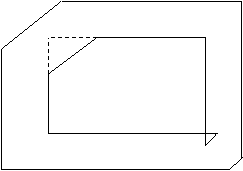
While doing this, some problems may
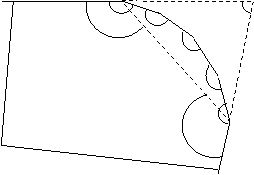
occur during combining of these lines. Small triangles, as seen in Figure 9,
may appear on drawings depending on shape of parcels.
At this situation, points causing
this kind of problems are eliminated by deleting these triangles. For this,
cutting points of parallel lines are determinated,
and then, distances from line end points to cutting points are added together.
If total distance value found is greater than the line length, it is accepted
that no problem exist. But, if total distance value found is equal to the line
length, it is accepted that there is a problem at that corner of the drawing.
In this case, line points causing the problem are eliminated, and the cutting
point related to them is accepted as the lines end point instead of them.
|
Pa 3 4 2 building
1 Pb 6 5 parcel |
No problem case: |1Pa| + |Pa2| > |12| Problem case: |1Pb| + |Pb6| = |16| |
Figure
9: Determining corner points of a building drawing
4. CONCLUSIONS
Preparation of plans
of building boundaries within a parcel in a fully automated manner necessitates
creation of carefully designed algorithms and databases. It is shown in this
paper work that once these designs are completed, this most time consuming and
much care needed engineering work turns out to be a
simple job.
REFERENCES
Banger, G., Bilgisayar Programlamanın Temel Bilgileri,
Baz,
Karagülle, İ.,Pala,Z.,
Visual Basic 6.0 Pro, Türkmen Kitabevi,
İstanbul, 1999
Korte, G., The GIS
book, pp. 23-35, Pub. By OnWord Press,
Uysal, M., MS Visual Basic ile yazılım
Geliştirme, Beta yayınevi,
İstanbul, 1997
Yanık, M., Visual Basic 5.0, İstanbul, 1997